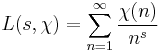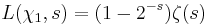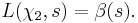Dirichlet character
In number theory, Dirichlet characters are certain arithmetic functions which arise from completely multiplicative characters on the units of 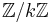 . Dirichlet characters are used to define Dirichlet L-functions, which are meromorphic functions with a variety of interesting analytic properties. If
. Dirichlet characters are used to define Dirichlet L-functions, which are meromorphic functions with a variety of interesting analytic properties. If 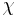 is a Dirichlet character, one defines its Dirichlet L-series by
is a Dirichlet character, one defines its Dirichlet L-series by
where s is a complex number with real part > 1. By analytic continuation, this function can be extended to a meromorphic function on the whole complex plane. Dirichlet L-functions are generalizations of the Riemann zeta-function and appear prominently in the generalized Riemann hypothesis.
Dirichlet characters are named in honour of Johann Peter Gustav Lejeune Dirichlet.
Contents |
Axiomatic definition
A Dirichlet character is any function χ from the integers to the complex numbers which has the following properties:
- There exists a positive integer k such that χ(n) = χ(n + k) for all n.
- If gcd(n,k) > 1 then χ(n) = 0; if gcd(n,k) = 1 then χ(n) ≠ 0.
- χ(mn) = χ(m)χ(n) for all integers m and n.
From this definition, several other properties can be deduced. By property 3), χ(1)=χ(1×1)=χ(1)χ(1). Since gcd(1, k) = 1, property 2) says χ(1) ≠ 0, so
- χ(1) = 1.
Properties 3) and 4) show that every Dirichlet character χ is completely multiplicative.
Property 1) says that a character is periodic with period k; we say that χ is a character to the modulus k. This is equivalent to saying that
- If a ≡ b (mod k) then χ(a) = χ(b).
If gcd(a,k) = 1, Euler's theorem says that aφ(k) ≡ 1 (mod k) (where φ(k) is the totient function). Therefore by 5) and 4), χ(aφ(k)) = χ(1) = 1, and by 3), χ(aφ(k)) =χ(a)φ(k). So
- For all a relatively prime to k, χ(a) is a φ(k)-th complex root of unity.
The unique character of period 1 is called the trivial character. Note that any character vanishes at 0 except the trivial one, which is 1 on all integers.
A character is called principal if it assumes the value 1 for arguments coprime to its modulus and otherwise is 0. A character is called real if it assumes real values only. A character which is not real is called complex.
The sign of the character χ depends on its value at −1. Specifically, χ is said to be odd if χ(−1) = −1 and even if χ(−1) = 1.
Construction via residue classes
Dirichlet characters may be viewed in terms of the character group of the unit group of the ring Z/kZ, as given below.
Residue classes
Given an integer k, one defines the residue class of an integer n as the set of all integers congruent to n modulo k: 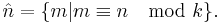 That is, the residue class
That is, the residue class 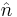 is the coset of n in the quotient ring Z/kZ.
is the coset of n in the quotient ring Z/kZ.
The set of units modulo k forms an abelian group of order 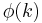 , where group multiplication is given by
, where group multiplication is given by 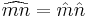 and
and  again denotes Euler's phi function. The identity in this group is the residue class
again denotes Euler's phi function. The identity in this group is the residue class 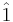 and the inverse of
and the inverse of 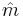 is the residue class
is the residue class 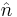 where
where 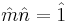 , i.e.,
, i.e.,  . For example, for k=6, the set of units is
. For example, for k=6, the set of units is 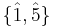 because 0, 2, 3, and 4 are not coprime to 6.
because 0, 2, 3, and 4 are not coprime to 6.
Dirichlet characters
A Dirichlet character modulo k is a group homomorphism 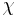 from the unit group modulo k to the non-zero complex numbers
from the unit group modulo k to the non-zero complex numbers
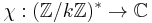 ,
,
necessarily with values that are roots of unity since the units modulo k form a finite group. We can lift 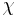 to a completely multiplicative function on integers relatively prime to k and then to all integers by extending the function to be 0 on integers having a non-trivial factor in common with k. The principal character
to a completely multiplicative function on integers relatively prime to k and then to all integers by extending the function to be 0 on integers having a non-trivial factor in common with k. The principal character 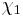 modulo k has the properties
modulo k has the properties
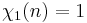 if gcd(n, k) = 1 and
if gcd(n, k) = 1 and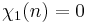 if gcd(n, k) > 1.
if gcd(n, k) > 1.
When k is 1, the principal character modulo k is equal to 1 at all integers. For k greater than 1, the principal character modulo k vanishes at integers having a non-trivial common factor with k and is 1 at other integers.
A few character tables
The tables below help illustrate the nature of a Dirichlet character. They present all of the characters from modulus 1 to modulus 10. The characters χ1 are the principal characters.
Modulus 1
There is 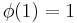 character modulo 1:
character modulo 1:
-
χ \ n 0 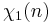
1
This is the trivial character.
Modulus 2
There is 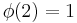 character modulo 2:
character modulo 2:
-
χ \ n 0 1 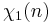
0 1
Note that χ is wholly determined by χ(1) since 1 generates the group of units modulo 2.
Modulus 3
There are 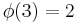 characters modulo 3:
characters modulo 3:
-
χ \ n 0 1 2 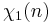
0 1 1 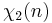
0 1 −1
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 3.
Modulus 4
There are 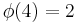 characters modulo 4:
characters modulo 4:
-
χ \ n 0 1 2 3 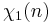
0 1 0 1 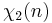
0 1 0 −1
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 4.
The Dirichlet L-series for 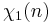 is the Dirichlet lambda function (closely related to the Dirichlet eta function)
is the Dirichlet lambda function (closely related to the Dirichlet eta function)
where 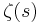 is the Riemann zeta-function. The L-series for
is the Riemann zeta-function. The L-series for 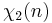 is the Dirichlet beta-function
is the Dirichlet beta-function
Modulus 5
There are 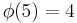 characters modulo 5. In the tables, i is a square root of
characters modulo 5. In the tables, i is a square root of 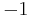 .
.
-
χ \ n 0 1 2 3 4 
0 1 1 1 1 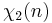
0 1 i −i −1 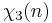
0 1 −1 −1 1 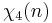
0 1 −i i −1
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 5.
Modulus 6
There are 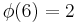 characters modulo 6:
characters modulo 6:
-
χ \ n 0 1 2 3 4 5 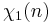
0 1 0 0 0 1 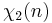
0 1 0 0 0 −1
Note that χ is wholly determined by χ(5) since 5 generates the group of units modulo 6.
Modulus 7
There are 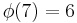 characters modulo 7. In the table below,
characters modulo 7. In the table below, 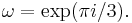
-
χ \ n 0 1 2 3 4 5 6 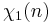
0 1 1 1 1 1 1 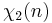
0 1 ω2 ω −ω −ω2 −1 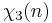
0 1 −ω ω2 ω2 −ω 1 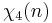
0 1 1 −1 1 −1 −1 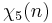
0 1 ω2 −ω −ω ω2 1 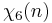
0 1 −ω −ω2 ω2 ω −1
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 7.
Modulus 8
There are 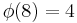 characters modulo 8.
characters modulo 8.
-
χ \ n 0 1 2 3 4 5 6 7 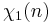
0 1 0 1 0 1 0 1 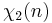
0 1 0 1 0 −1 0 −1 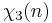
0 1 0 −1 0 1 0 −1 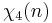
0 1 0 −1 0 −1 0 1
Note that χ is wholly determined by χ(3) and χ(5) since 3 and 5 generate the group of units modulo 8.
Modulus 9
There are 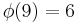 characters modulo 9. In the table below,
characters modulo 9. In the table below, 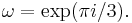
-
χ \ n 0 1 2 3 4 5 6 7 8 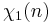
0 1 1 0 1 1 0 1 1 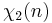
0 1 ω 0 ω2 −ω2 0 −ω −1 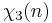
0 1 ω2 0 −ω −ω 0 ω2 1 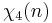
0 1 −1 0 1 −1 0 1 −1 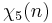
0 1 −ω 0 ω2 ω2 0 −ω 1 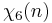
0 1 −ω2 0 −ω ω 0 ω2 −1
Note that χ is wholly determined by χ(2) since 2 generates the group of units modulo 9.
Modulus 10
There are 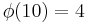 characters modulo 10.
characters modulo 10.
-
χ \ n 0 1 2 3 4 5 6 7 8 9 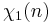
0 1 0 1 0 0 0 1 0 1 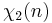
0 1 0 i 0 0 0 −i 0 −1 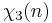
0 1 0 −1 0 0 0 −1 0 1 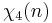
0 1 0 −i 0 0 0 i 0 −1
Note that χ is wholly determined by χ(3) since 3 generates the group of units modulo 10.
Examples
If p is a prime number, then the function
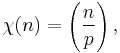 where
where 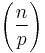 is the Legendre symbol, is a Dirichlet character modulo p.
is the Legendre symbol, is a Dirichlet character modulo p.
More generally, if m is an odd number the function
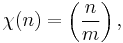 where
where 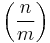 is the Jacobi symbol, is a Dirichlet character modulo m. These are called the quadratic characters.
is the Jacobi symbol, is a Dirichlet character modulo m. These are called the quadratic characters.
Conductors
Residues mod N give rise to residues mod M, for any factor M of N, by discarding some information. The effect on Dirichlet characters goes in the opposite direction: if χ is a character mod M, it gives rise to a character χ* mod N for any multiple N of M. With some attention to the values at which characters take the value 0, one gets the concept of a primitive Dirichlet character, one that does not arise from a factor; and the associated idea of conductor, i.e. the natural (smallest) modulus for a character. Imprimitive characters can cause missing Euler factors in L-functions.
History
Dirichlet characters and their L-series were introduced by Johann Peter Gustav Lejeune Dirichlet, in 1831, in order to prove Dirichlet's theorem on arithmetic progressions. He only studied them for real s and especially as s tends to 1. The extension of these functions to complex s in the whole complex plane was obtained by Bernhard Riemann in 1859.
See also
References
- See chapter 6 of Apostol, Tom M. (1976), Introduction to analytic number theory, Undergraduate Texts in Mathematics, New York-Heidelberg: Springer-Verlag, ISBN 978-0-387-90163-3, MR0434929
- Spira, Robert (1969). "Calculation of Dirichlet L-Functions". Mathematics of Computation 23 (107): 489–497. doi:10.1090/S0025-5718-1969-0247742-X. MR0247742.
- Apostol, T. M. (1971). "Some properties of completely multiplicative arithmetical functions". The American Mathematical Monthly 78 (3): 266–271. doi:10.2307/2317522. JSTOR 2317522. MR0279053.
- Hasse, Helmut (1964). Vorlesungen über Zahlentheorie. Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen. Springer. MR0188128. see chapter 13.